What is the Golden Ratio?
The Golden Ratio is a mathematical concept representing the ratio between two unequal numbers, where the more significant number relates to the smaller one in the same way that the sum of these numbers relates to the more substantial number. The Golden Ratio is approximately equal to 1.618, or 1.62 when rounded, and it is symbolized by the Greek letter φ, “phi,” named after the ancient Greek sculptor Phidias. It is believed that he used such proportions in the design of the Parthenon.
The most well-known graphical representations of the Golden Ratio include a rectangle with dimensions approximately 62:48 and a spiral constructed within it.
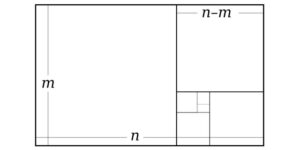
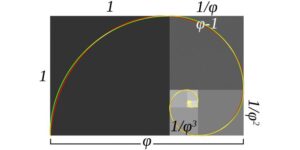
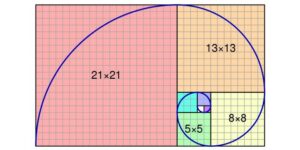
The Golden Ratio is closely related to the Fibonacci numbers, a series of numbers where each is the sum of the two preceding ones: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on. The further this series progresses, the closer the ratio of adjacent numbers approaches 1.618. For example, 3/2 = 1.5; 8/5 = 1.6, and 34/21 = 1.619.
Why is the Golden Ratio so famous?
Ancient Greek mathematicians, such as Pythagoras and Euclid, were the first to take an interest in the Golden Ratio. They believed the entire universe was built upon numbers and that any phenomenon could be explained using them. It’s not surprising that this elegant ratio intrigued ancient thinkers.
Following them, the Golden Ratio fascinated many prominent scientists and artists. Examples include Leonardo da Vinci, Albrecht Dürer, Johannes Kepler, Le Corbusier, Salvador Dalí, and Richard Penrose.
It’s considered the “divine proportion.”
The term “Golden Ratio” was coined by the 19th-century German mathematician Martin Ohm. Beforeim, this ratio was recalledhe “divine proportion.”
Because of the attributes attributed to it, the Golden Ratio was frequently employed as much as possible. During the Renaissance, for instance, this number was considered the ideal choice for determining dimensions. For example, the “Golden Rectangle” was often used in creating books and paintings. The waistline was even called the boundary of the Golden Ratio in the human body.
Some still consider this proportion a secret of attractiveness and an example of universal harmony pleasing the human eye. Plastic surgeons, for instance, like to talk about the Golden Ratio. Furthermore, this number is popular in mathematics like no other.
It can be found in nature.
Fibonacci numbers and spirals resembling the Golden Ratio are frequently found in nature. For instance, in the number of petals on flowers or the shape of plants.

It is found in architectural and artistic works.
For example, “divine proportions” can be found in the Parthenon and Egyptian pyramids. There is also a widespread misconception that the “Mona Lisa” was painted according to the Golden Ratio.
Why the universality of the Golden Ratio is a myth.
However, upon careful examination, it becomes clear that this proportion is not as all-encompassing as it is often portrayed.
The divinity of the Golden Ratio is exaggerated.
The importance attributed to the Golden Ratio is more significant than it deserves. Beautiful patterns and an aura of mystery have turned this ordinary geometric ratio into a mathematical myth that numerologists love.
Most of the time, things are attributed to the Golden Ratio with significant assumptions. In such cases, there is no need to talk about accuracy and mathematical universality. Therefore, one can find “divine proportions” anywhere with a desire.
The Golden Ratio is not as widespread.
It is not found everywhere. For example, poppies always have four petals, which do not fit into the Fibonacci sequence. Additionally, four-leaf clovers are pretty standard. The shells of marine mollusks resemble the spiral of the Golden Ratio, but they are still different. They have more turns, and the distance between them is smaller. The coefficient of shell spiraling in no mollusk comes close to 1.62. This can even be seen with the naked eye.

In the human body, there are so many points for measurement that, if desired, one can find the Golden Ratio anywhere. However, with a high probability, different people will have to look for the “divine proportion” in other places, as we can vary significantly.
In art, it is not so common.
Studying 565 paintings by prominent artists revealed that, on average, the aspect ratio in their works was 1.34. This falls short of the Golden Ratio. Scientists cannot even find it in the works of Leonardo da Vinci.
Archaeological research does not confirm that ancient Greeks used the Golden Ratio to construct the Parthenon. Out of more than 100 monuments of ancient Greek architecture, this number was found in the proportions of only four objects: a tower, an altar, a tomb, and a memorial. The ancient Egyptians could not have used the Golden Ratio either, as they did not have the necessary technology to calculate proportions precisely.
Who can benefit from the Golden Ratio in reality?
Modern mathematics uses the Golden Ratio and Fibonacci numbers to describe fractals—figures that exhibit self-similarity.

Knowledge of the number φ is crucial in studying chaos and dynamical systems. It helps us understand how nature develops and self-organizes.
Additionally, Fibonacci numbers help solve some complex issues. For example, using these numbers, Soviet mathematician Yuri Matiyasevich proved that there is no universal algorithm for solving equations with at least two unknowns.

